The math of logistic classifier

26 Aug 2017

This post demonstrates the mathematical model behind logistic regression, which serves as the building block of the deep learning. I write this post to help others understand deep learning, I also write it for myself to learn deep learning more deeply.

Model after biological neuron

Modern deep learning techniques model after biological cognition, the basic unit of which is neuron. It is the building block of deep learning starts with neuron-inspired math modeling using logistic regression. The math behind a simple logistic regression classifier looks like below:

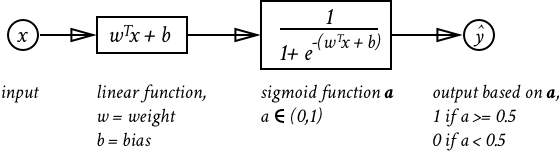
Image this function represents a neuron in your brain, the input is the stimulus your brain received (sound, touch, etc.), represented by the data captured in $x$; and the output is a binary decision of whether that neuron gets triggered or not, represented by the binary value of $\hat{y}$.

In order to have the neuron work properly, we need to have decent value for weights and bias terms, denoted as $w$ and $b$ respectively. However, we don’t have good values for $w$ nor $b$ automatically, we need to train our model and acquire good weights and bias terms. Image our function as a newborn baby, and it takes training to teach a baby to walk, speak etc. We need to train our neuron model and figure out good values for $w$ and $b$.

So the question is how to train for logistic regression? Given we have a set of training dataset, we can measure the error of our current model by comparing predicted value and actual value, then take the result to do better. We can break down the question of how to train for logistic regression into a set of smaller problems:

• question 1: how to define the error of predictions from our model?
• question 2: how to take the error to refine our model?

The technique to address question 1 is called forward propagation, and the technique to address question 2 is called backward progation.

Forward Propagation

Forward progation enables two things. First, it provides a predicted value $\hat{y}$ based on the input $x$. To break down the calculation mathematically:

• $z^{(i)} = w^{T}x^{(i)} + b$
• $a^{(i)} = \frac{1}{1+ e^{-z^{(i)}}}$

If the value of $a^{(i)}$ is greater than or equal to 0.5, then $y^{(i)}$ is predicted as 1, otherwise $y^{(i)}$ is 0.

Second, it allows the model to calculate an error based on a loss function, this error quantifies how well our current model is performing using $w$ and $b$. The loss function for the logistic regression is below:

• $\iota(a, y) = ylog(a) + (1 - y)log(1-a)$

How does this loss function makes sense? The way I think about is that if the prediction is close to actual value, the value should be low. If the prediction is far from actual value, the value should be high. Gi

cost function based on loss function

Next we define a cost function for the entire dataset based on the loss function because we have many rows of training data, say $m$ records. The value of the error based on the cost function is avaraged out across all errors:

• $\iota(a^{(i)}, y^{(i)}) = - \frac{1}{m} \sum_{i=1}^{m} y^{(i)}log(a^{(i)}) + (1 - y^{(i)})log(1-a^{(i)})$
• $J = \frac{1}{m}\sum_{i=1}^{m}\iota(a^{(1)}, y^{(i)})$

Given we have a way to measure the error of our prediction model, we can set the goal to minimize prediction error by adjusting our model parameters, and this is where backward propagation comes in.

Backward Propagation

To tackle the problem of how to refine our model to reduce training error, we can more formally define our problem as following:

1. Given a dataset $X$
2. The model computes $A = \sigma(w^T X + b) = (a^{(0)}, a^{(1)}, ..., a^{(m-1)}, a^{(m)})$
3. The model calculates the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
4. Apply cost function $J$ to adjust $w$ and $b$

To implement step 4, we need to apply gradient descent.

Gradient Descent

Quote from Wikipedia on gradient descent:

Gradient descent is a first-order iterative optimization alogirthm for finding the minimum of a function.

Great! We want to find the minimum of our cost function by adjusting $w$ and $b$. Following the gradient descent algorithm, we take the following steps:

1. taking partial derivatives off our parameters, which tells us the delta values of adjusting that value
2. update our parameters based on the delta value from the partial derivatives

The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $\theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.

Translate the steps above mathematically, we get:

update w

• $\frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T$
• $w := w - \alpha\frac{\partial J}{\partial w}$

update b

• $\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} (a^{(i)}-y^{(i)})$
• $b := b - \alpha\frac{\partial J}{\partial b}$

Put it all togher

We can now have a big picture of how we want to use logistic regression classifier to predict future dataset based on training dataset. A high-level architectural steps can be summarized as:

1. Gather training dataset $(X_{train}, Y_{train})$ and test dataset $(X_{test}, Y_{test})$.
2. Initialize model parameters $w$ and $b$.
3. Define learning rate $\alpha$, and number of training iterations.
4. For each training iteration, run through:
   • apply forward propagation with $(X_{train}, Y_{train})$, $w$ and $b$
   • calculate cost funtion $J$
   • apply backward propagation to adjust $w$ and $b$
5. Verify the accuracy of the model using $(X_{test}, Y_{test})$

tech

---