The math of neural networks

05 Sep 2017

Building neural networks is at the heart of any deep learning technique. Neural networks is a series of forward and backward propagations to train paramters in the model, and it is built on the unit of logistic regression classifiers. This post will expand based on the math of logistic regression to build more advanced neural networks in mathematical terms.

A neural network is composed of layers, and there are three types of layers in a neural network: one input layer, one output layer, and one or many hidden layers. Each layer is built based on the same structure of logistic regression classifier, with a linear transformation and an activation function. Given a fixed set of input layer and output layer, we can build more complex neural network by adding more hidden layers.

Before diving into the details of the mathematical model, we need to have a big picture of the computation. To quote from deeplearning.ai class:

the general methodology to build a Neural Network is to:

Define the neural network structure (number of input units, number of hidden units, etc.)

Initialize the model’s parameters

Loop

• Implement forward propagation
• Compute loss
• Implement backward propagation to get the gradients
• Update parameters (gradients)

To make it easier to understand, we take an iterative approach to break down the math of neural networks, first we analyze a 2-layer neural network, then we analyze L-layer neural network.

Two-layer neural network

Let’s think of the following hypothetical scenario: we have two nodes $x_{1}$ and $x_{2}$ for input layer, three nodes defined in the hidden layer, and we have one node $y$ for the output layer. Converting the graph below into mathematical terms, we have:

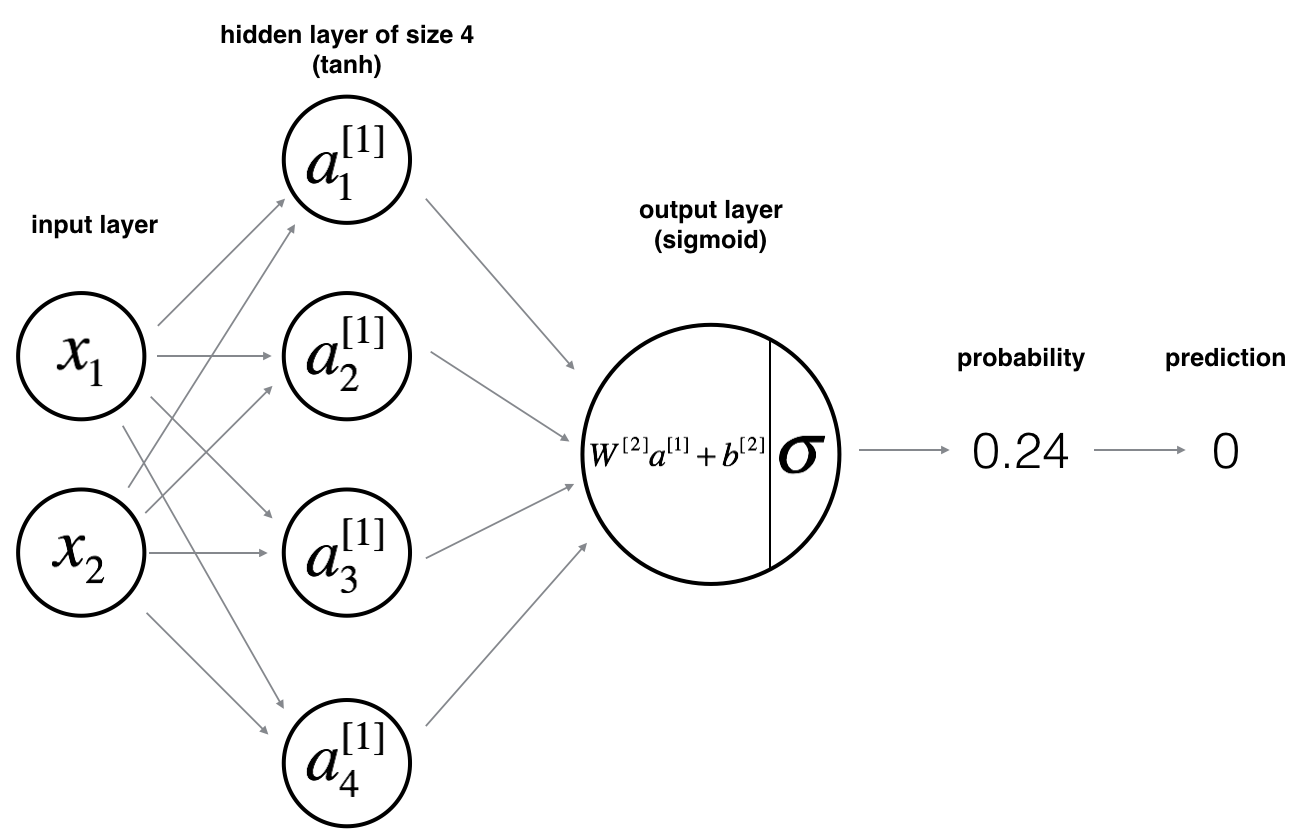
The following is our input parameters where we specify the 2-layer neural network:

1. Input layer $X \in (2, 1)$, with its weight $W_{1}$ and bias $b_{1}$
2. Oput layer $Y \in (1, 1)$, with its weight $W_{2}$ and bias $b_{2}$
3. Hidden layer $A \in (4, 1)$

To perform forward propagation, we have the following calculation:

• $z^{[1]} = W^{[1]} x^{(i)} + b^{[1]}$
• $a^{[1]} = \tanh(z^{[1]})$
• $z^{[2]} = W^{[2]} a^{[1]} + b^{[2]}$
• $\hat{y}^{(i)} = a^{[2]} = \sigma(z^{[2]})$
• If $a^{[2]} > 0.5$ then $\hat{y}^{(i)} = 1$, otherwise $\hat{y}^{(i)} = 0$.

Given that we have computed $A^{[2]}$, which contains $a^{[2](i)}$ for every example, we can compute the cost function as follows:

• $J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2](i)}\right) + (1-y^{(i)})\log\left(1- a^{[2](i)}\right) \large{)} \small$

Given the loss function, we want to implement the backward propagation starting from $z_{2}$ back to $z_{1}$:

• $dz^{[2]} = a^{[2]} - y$
• $dW^{[2]} = dz^{[2]}(a^{[1]})^{T}$
• $db^{[2]} = dz^{[2]}$
• $dz^{[1]} = (W^{[2]})^{T}dz^{[2]} * g^{[1]'}(z^{[1]})$
• $dW^{[1]} = dz^{[1]}x^{T}$
• $db^{[1]} = dz^{[1]}$

Then we use gradient descent to calculate $W^{[1]}$, $b^{[1]}$ and $W^{[2]}$, $b^{[2]}$, with a specified learning rate $\alpha$:

• $W^{[1]} = W^{[1]} - \alpha * dW^{[1]}$
• $b^{[1]} = b^{[1]} - \alpha * db^{[1]}$
• $W^{[2]} = W^{[2]} - \alpha * dW^{[2]}$
• $b^{[2]} = b^{[2]} - \alpha * db^{[2]}$

After one iteration of the loop is finished, we then run the model again with the training set, and we expect to see the value of loss function descreases.

L-layer neural network

A l-layer neural network follows the same logical loop as the 2-layer neural network, however activation function for the hidden layers is different.

Rather than using $tanh$ as the activation function, in recent years people have started using rectified linear function, ReLU for short. ReLU has two advantages, first is that it is a non-linear function so it provides the similar benefit as other non-linear function such as $tanh$ or $sigmoid$. Also, the derivative of ReLU is a constant, making it much faster when calculating the backward propagation step.

In addition, we need to make sure we initialize non-zero values for $W^{[1]}$. if $W^{[1]}$ is a vector of zeros, then the forward and backward propagation will effectively update parameters during each iteration, making the model ineffective.

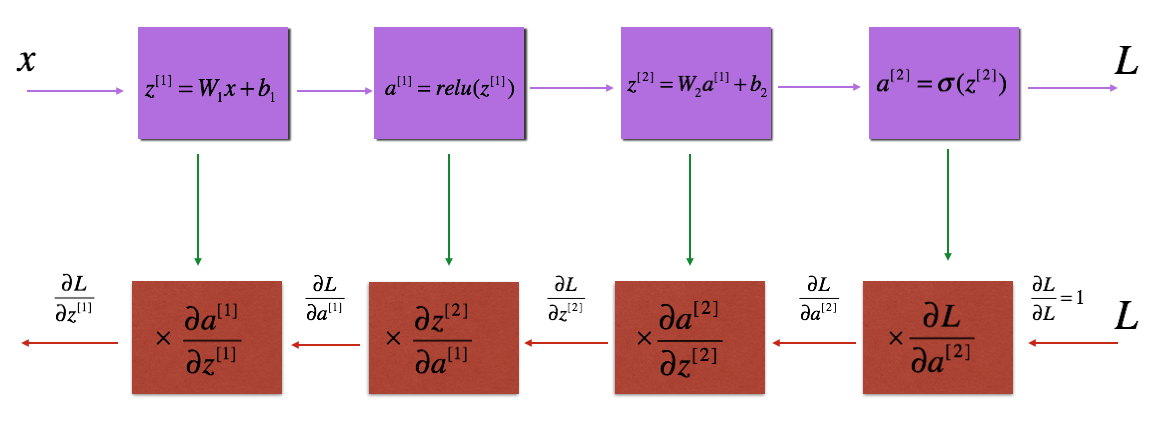
Following the general pattern of building the neural network, we can specify the input parameters in mathmatical terms:

• We have $L$ layers with input layer $X$ and output layer $Y$.

The forward propagation is computed using following equations:

• The first activation layer: $Z^{[1]} = W^{[1]}X + b^{[1]}$, $A^{[1]} = ReLU(Z^{[1]})$
• The nth activation layer: $Z^{[n]} = W^{[n]}A^{[n-1]} + b^{[1]}$, $A^{[n]} = ReLU(Z^{[n]})$
• The last activation layer: $Z^{[L]} = W^{[L]}A^{[L-1]} + b^{[1]}$, $A^{[n]} = sigmoid(Z^{[L]})$

Next we want to implement the loss function to check if our model is actually learning:

$-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right))$

Then we calculate the backward propagation, which follows steps similar to forward propagation:

• linear backward
• linear to activation backward where activation computes the derivative of $ReLU$ or $sigmoid$ activation
• [linear to $ReLU$] X (L-1) to Linear to $sigmoid$ backward (whole model)

For layer $l$, the linear part is: $Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}$ (followed by an activation).

Given we have already calculated the derivative $dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}}$. We want to get $(dW^{[l]}, db^{[l]} dA^{[l-1]})$.

• $dW^{[l]} = \frac{\partial \mathcal{L} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T}$
• $db^{[l]} = \frac{\partial \mathcal{L} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}$
• $dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]}$

Now that we have $(dW^{[l]}, db^{[l]} dA^{[l-1]})$, we can update our parameters using gradient descent:

• $W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}$
• $b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]}$

Similar to 2 layer neural network, after one iteration of the loop is finished, we then run the model again with the training set, and we expect to see the value of loss function descreases.

tech

---